(Crossposted from the AI Alignment Forums)

I’m worried about scenarios involving deceptive models. We’ve failed at inner alignment so the model has goals that are not aligned with ours. It can somehow detect when it’s in training, and during training it pretends to share our goals. During deployment, surprise! The model paperclips the universe.

In this story deception is all about the model having hidden behaviors that never get triggered during training. There are many inputs where the model does what we want. These correspond to inputs where it ‘plays along’. Then on some rare input or an input outside of the training distribution it defects, triggering some catastrophic behavior that corresponds to maximizing an ulterior motive.

This suggests that we should be wary of models that have logic/subcircuits/states that are never used during training, and we can penalize models for having such hidden behaviors.

In the rest of this post I’ll flesh out a family of priors that penalize hidden behaviors, which I think provide at least a few bits of optimization away from deception. These are very much working notes, and feedback is very welcome.

One-Gate Trace Prior: Entropy

Consider a boolean circuit. The output of each gate is 0/1. One way to implement the entropy prior is to record traces of these outputs during training, and penalize the model for having strong bias between 0/1:

$$ p \propto e^{-\sum_i \sum_{j\in [0,1]} p_i(j) \ln p_i(j)} $$

Here $p_i$ is the observed fraction of the time gate $i$ produced output $j$ during training. I call this the one-gate trace prior because it only relies on probabilities defined over single gates. This prior favors models where each gate has even odds of outputting 0/1.

The intuition for why this might work is that deceptive models need some machinery specifying when and how they defect, and this machinery is never active during training. This is at the core of what makes them bad! If the defecting machinery activated during training we’d notice because the model would stop optimizing the outer goal, so we’d assign it a high loss and move on to better models.

Another framing is: It is inherently suspicious if a model has machinery that is rarely activated. That machinery wasn’t vetted during training, so we have no reason to trust it. If the model has a hidden love of paperclips, this is the natural place to hide it.

As a technical detail, in order to do useful computation the model may need access to some constant input wires, and these should be excluded from the prior.

Normalization

The one-gate trace prior isn’t normalized, and can’t be normalized without an additional prior over e.g. complexity. So in reasoning about it we need to remember that there will always be another piece to the prior setting the distribution over circuits. I’m agnostic to the details of that prior, and view the one-gate trace prior as a regularizer we apply to other (normalized) priors to make them safer.

Objection: Model Performance

This prior could cause a performance hit. The intuition is that sometimes a model will need to respond to unusual events even in the training distribution, so forcing the distribution over gate outputs to be as uniform as possible could make it hard to act in environments containing rare events.

In particular, this prior disfavors modularity. Suppose the model is meant to classify images. It might be natural have separate sub-circuits for recognizing cats and dogs. If cats are much more likely than dogs during training, our prior will disfavor models that separate that machinery out, because the ‘dog’ sub-circuit will rarely be active and the ‘cat’ sub-circuit will often be active.

If the pressure to perform well during training is strong enough this could push models towards obfuscating their calculations just to hide from the prior, which is bad.

Patch: Don’t use entropy

We can make our prior more forgiving of modularity and biased inputs by just disfavoring really rarely activations, e.g.

$$ p \propto e^{-\sum_i \sum_{j\in [0,1]} p_i(j)^m} $$

Here $m$ is a positive number, and as we make $m$ large the prior becomes indifferent to the middle of the probability distribution. For example, below I’ve plotted $-(p^{m}+(1-p)^{m})$ over [0,1] for $m=20$.

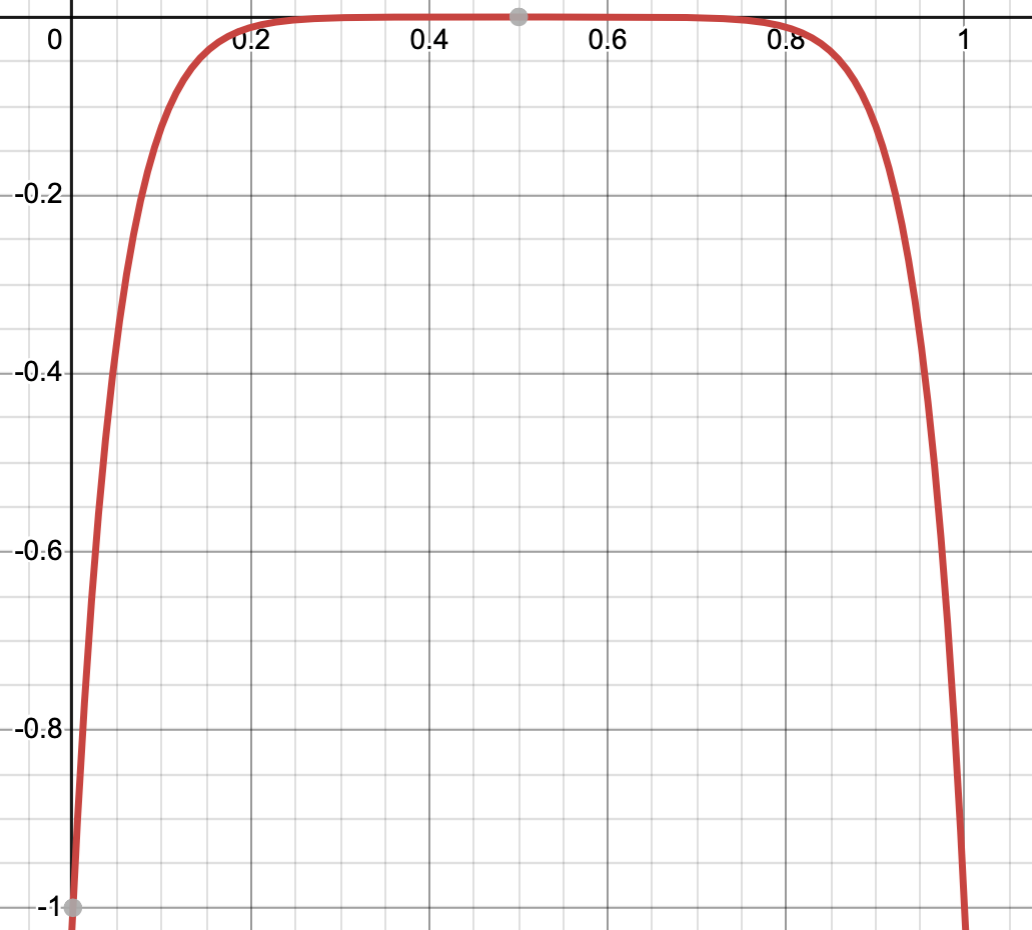
How should we pick $m$? We just want assurances that all the gears in the model got tried out at least a few times during training. So we’re looking to see that each gate produced each output at least $q$ times during training, where $q$ is fixed.

Suppose we have $N$ training samples. We want our prior to be flat over $[q/N,1-q/N]$ and to penalize models outside that window, which means $m \sim \log N/q$. That is, as we get more data we can make our prior indifferent to larger windows because we’re able to observe rarer behavior.

In this framing, $q$ is a sort of safety parameter: larger $q$ means the prior is more suspicious of uneven distributions and requires that we see more examples before we trust the model.

Relation to Performance

This patch resolves the performance issues we saw using entropy. Modular circuits are totally fine under this prior so long as they all get checked out during training. Even if dog images come up less often than cat images, they still have to come up a decent number of times for us to be confident the model has learned what a dog is, and if that number is at least $q$ then we won’t penalize the model for having separate dog and cat circuits.

Implementation

A naive way to implement this prior is to run each circuit $N$ extra times per training evaluation, and to use traces from those extra evaluations to compute the prior. This is obviously expensive if we make $N$ large, though only linearly so.

If we’re dealing with a neural network instead of a boolean circuit we can reinforce pathways taken during training. Specifically, the first $q$ times a neuron is active (has a positive sum), and the first $q$ times it is inactive, we reinforce all weights emerging from that neuron.

As a technical detail, activations early in training probably shouldn’t ‘count’ as exploring the model’s behavior space. That can probably be addressed by only tracking the most recent $N$ training samples when evaluating if a given neuron has activated $q$ times.

Objection: Moving Computation

One way that deception can hide from this prior is by changing the location on the circuit where the deceptive conditional (”Am I in training or deployment?”) gets evaluated. For instance if the model can make this conditional get evaluated in different places in the circuit depending on the inputs it receives, it is no longer helpful to compare the behavior of any single gate across evaluations.

This actually seems like a very big problem, because only takes a small number of bits of model complexity to make the relevant evaluation shift around on the circuit. In a future post I’ll flesh out this failure mode further, and consider additional patches.

Summary

Training trace priors provide a way of looking for hidden behaviors, which are signs of deception. This makes them very closely related to methods of fuzzing, where automated systems try to explore the space of program behaviors.

The specific priors I’ve constructed above are probably not too helpful on their own, but my hope is that there is a version of a trace prior that more strongly pushes away from deception.

(Thanks to Evan Hubinger and Nicholas Schiefer for suggestions and discussions around these ideas)